
Numerical Methods in Physics
Advanced computational techniques for solving complex physical systems using Python and modern numerical libraries. A comprehensive guide to finite difference, Monte Carlo, spectral methods, and more.

Advanced computational techniques for solving complex physical systems using Python and modern numerical libraries. A comprehensive guide to finite difference, Monte Carlo, spectral methods, and more.
This research paper presents a comprehensive analysis of numerical methods for solving complex physical systems. We explore the implementation, accuracy, stability, and computational efficiency of various numerical techniques using modern Python libraries including NumPy, SciPy, SymPy, and specialized physics packages.
Most physical phenomena are described by differential equations that cannot be solved analytically. Numerical methods provide approximate solutions that are essential for:
Schrödinger equation solutions
Navier-Stokes equations
Maxwell's equations
| Method | Type | Accuracy | Stability | Best For | Python Library |
|---|---|---|---|---|---|
| Finite Difference | Grid-based | Medium-High | Conditional | PDEs, Heat Eq. | NumPy |
| Finite Element | Mesh-based | High | Good | Complex geometries | FEniCS |
| Monte Carlo | Stochastic | Low-Medium | Excellent | High-dimensional | NumPy |
| Spectral Methods | Global | Very High | Good | Smooth solutions | SciPy |
| Runge-Kutta | ODE Solver | High | Excellent | Time integration | SciPy |
| Verlet Integration | Molecular Dynamics | Medium | Good | N-body problems | ASE |
Approximates derivatives using finite differences on a grid. Simple implementation but limited to regular geometries.
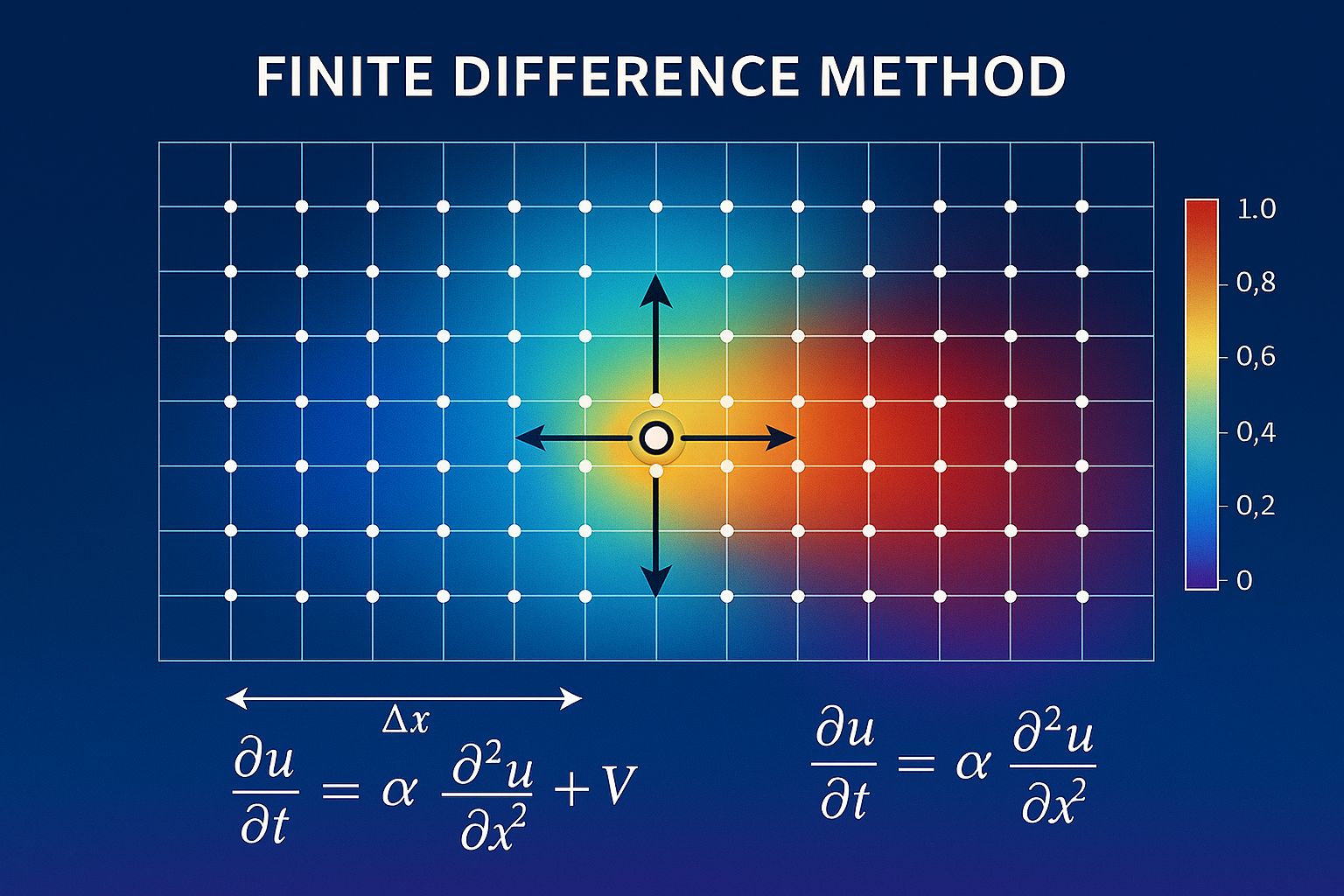
Finite difference grid with gradient calculations
Uses variational formulation and basis functions. Excellent for complex geometries but computationally intensive.
Uses random sampling to estimate solutions. Excellent for high-dimensional problems but slow convergence.
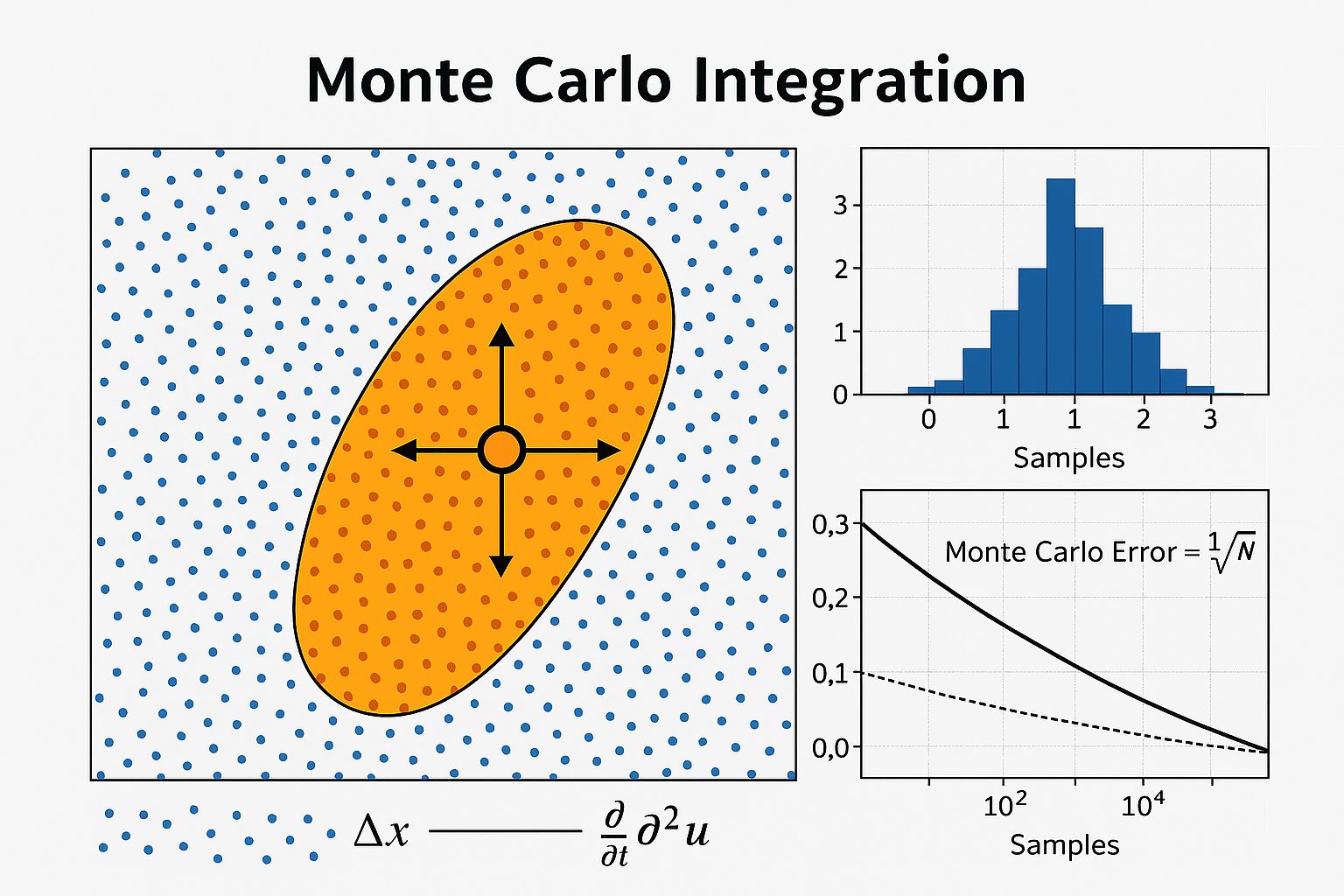
Monte Carlo random sampling with 1/√N error convergence

Python code with NumPy/SciPy for scientific computing
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
def solve_heat_equation_fd(L=1.0, T=0.5, alpha=0.01, nx=101, nt=1000):
"""
Solve 1D heat equation: ∂u/∂t = α ∂²u/∂x²
using finite difference method
"""
# Spatial grid
x = np.linspace(0, L, nx)
dx = x[1] - x[0]
# Time stepping
dt = T / nt
# Stability condition
r = alpha * dt / dx**2
if r > 0.5:
print(f"Warning: Unstable for r={r:.3f} > 0.5")
# Initial condition (Gaussian pulse)
u = np.exp(-100 * (x - 0.5)**2)
# Boundary conditions (Dirichlet: u=0 at ends)
u[0] = u[-1] = 0.0
# Store solutions for animation
solutions = [u.copy()]
# Finite difference scheme (explicit)
for n in range(nt):
u_new = u.copy()
for i in range(1, nx-1):
u_new[i] = u[i] + r * (u[i+1] - 2*u[i] + u[i-1])
u = u_new
if n % 100 == 0: # Store every 100th step
solutions.append(u.copy())
return x, solutions, dt
# Run simulation
x, solutions, dt = solve_heat_equation_fd()
# Create animation
fig, ax = plt.subplots(figsize=(10, 6))
line, = ax.plot(x, solutions[0], 'b-', linewidth=2)
ax.set_xlim(0, 1)
ax.set_ylim(0, 1)
ax.set_xlabel('Position (x)', fontsize=12)
ax.set_ylabel('Temperature (u)', fontsize=12)
ax.set_title('1D Heat Equation - Finite Difference Solution', fontsize=14)
ax.grid(True, alpha=0.3)
def animate(i):
line.set_ydata(solutions[i])
ax.set_title(f'Time: {i*100*dt:.3f} s')
return line,
ani = FuncAnimation(fig, animate, frames=len(solutions), interval=100)
plt.tight_layout()
plt.show()import numpy as np
import matplotlib.pyplot as plt
from scipy import integrate
import time
def monte_carlo_integrate(func, dim, n_samples=100000):
"""
Monte Carlo integration in arbitrary dimensions
∫ f(x) dx over [0,1]^dim
"""
# Generate random samples
samples = np.random.random((n_samples, dim))
# Evaluate function at sample points
values = func(samples)
# Calculate Monte Carlo estimate
volume = 1.0 # Volume of [0,1]^dim
integral_estimate = volume * np.mean(values)
# Estimate error (standard deviation of mean)
error_estimate = volume * np.std(values) / np.sqrt(n_samples)
return integral_estimate, error_estimate
def example_function_6d(x):
"""
6-dimensional example function:
f(x) = exp(-∑ (x_i - 0.5)^2)
"""
r_squared = np.sum((x - 0.5)**2, axis=1)
return np.exp(-10 * r_squared)
# Compare Monte Carlo with other methods
def compare_integration_methods():
dim = 6
n_samples = 100000
print(f"Integrating 6-dimensional function")
print(f"Monte Carlo samples: {n_samples:,}")
print("-" * 50)
# Monte Carlo integration
start_time = time.time()
mc_integral, mc_error = monte_carlo_integrate(
example_function_6d, dim, n_samples
)
mc_time = time.time() - start_time
# Quadrature (only works for low dimensions)
if dim <= 3:
start_time = time.time()
quad_result = integrate.nquad(
lambda *args: example_function_6d(np.array([args]).T),
[[0,1]]*dim
)[0]
quad_time = time.time() - start_time
print(f"Monte Carlo Result: {mc_integral:.6f} ± {mc_error:.6f}")
print(f"Monte Carlo Time: {mc_time:.3f} seconds")
print(f"Monte Carlo Efficiency: {n_samples/mc_time:.0f} samples/sec")
if dim <= 3:
print(f"\nQuadrature Result: {quad_result:.6f}")
print(f"Quadrature Time: {quad_time:.3f} seconds")
print(f"Speedup: {quad_time/mc_time:.1f}x faster")
# Error convergence analysis
print("\n" + "-" * 50)
print("Monte Carlo Error Convergence (1/√N):")
sample_sizes = [1000, 5000, 20000, 50000, 100000, 500000]
errors = []
for n in sample_sizes:
_, error = monte_carlo_integrate(example_function_6d, dim, n)
errors.append(error)
# Plot convergence
plt.figure(figsize=(10, 6))
plt.loglog(sample_sizes, errors, 'bo-', linewidth=2, markersize=8)
plt.loglog(sample_sizes, 1/np.sqrt(sample_sizes), 'r--',
linewidth=2, label='1/√N reference')
plt.xlabel('Number of Samples (N)', fontsize=12)
plt.ylabel('Error Estimate', fontsize=12)
plt.title('Monte Carlo Error Convergence (6D Integration)', fontsize=14)
plt.grid(True, alpha=0.3)
plt.legend()
plt.tight_layout()
plt.show()
# Run comparison
if __name__ == "__main__":
compare_integration_methods()Dimensional Independence
Error ~ 1/√N regardless of dimension
Parallel Friendly
Embarrassingly parallel computation
Complex Domains
Works with arbitrary integration regions
Solving the time-independent Schrödinger equation using finite differences to find energy eigenvalues and eigenfunctions.
# Simplified implementation
import numpy as np
from scipy.sparse import diags
from scipy.sparse.linalg import eigs
def solve_quantum_oscillator(n=1000, levels=5):
x = np.linspace(-10, 10, n)
dx = x[1] - x[0]
# Construct Hamiltonian matrix
T = diags([1, -2, 1], [-1, 0, 1], shape=(n, n)) / dx**2
V = diags(0.5 * x**2, 0)
H = -0.5 * T + V
# Find eigenvalues (energies)
eigenvalues, eigenvectors = eigs(H, k=levels, which='SR')
return np.real(eigenvalues), eigenvectors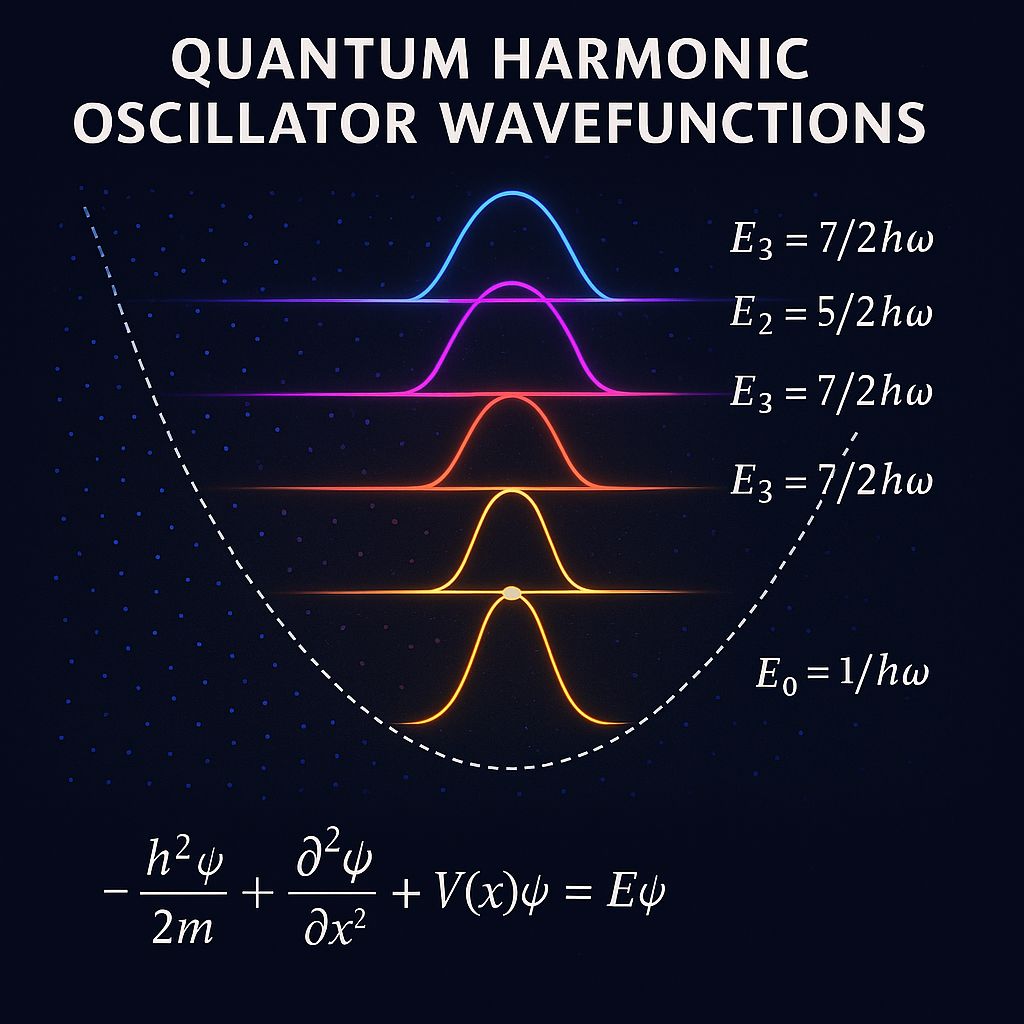
Quantum harmonic oscillator wavefunctions and energy levels
Implementing the incompressible Navier-Stokes equations using finite volume method with SIMPLE algorithm for pressure-velocity coupling.
# Core Navier-Stokes solver
def solve_navier_stokes(u, v, p, dt, dx, dy, nu, rho):
# Predictor step (momentum without pressure)
u_star = u + dt * (
-convective(u, v, dx, dy) +
nu * laplacian(u, dx, dy)
)
# Pressure Poisson equation
p = solve_pressure_poisson(u_star, v_star, dx, dy, dt, rho)
# Corrector step
u = u_star - dt * gradient(p, dx) / rho
v = v_star - dt * gradient(p, dy) / rho
return u, v, p
CFD simulation showing flow around a cylinder
Poisson equation solver for charge distributions using multigrid methods
N-body simulations using Runge-Kutta and symplectic integrators
3D transient heat conduction with complex boundary conditions
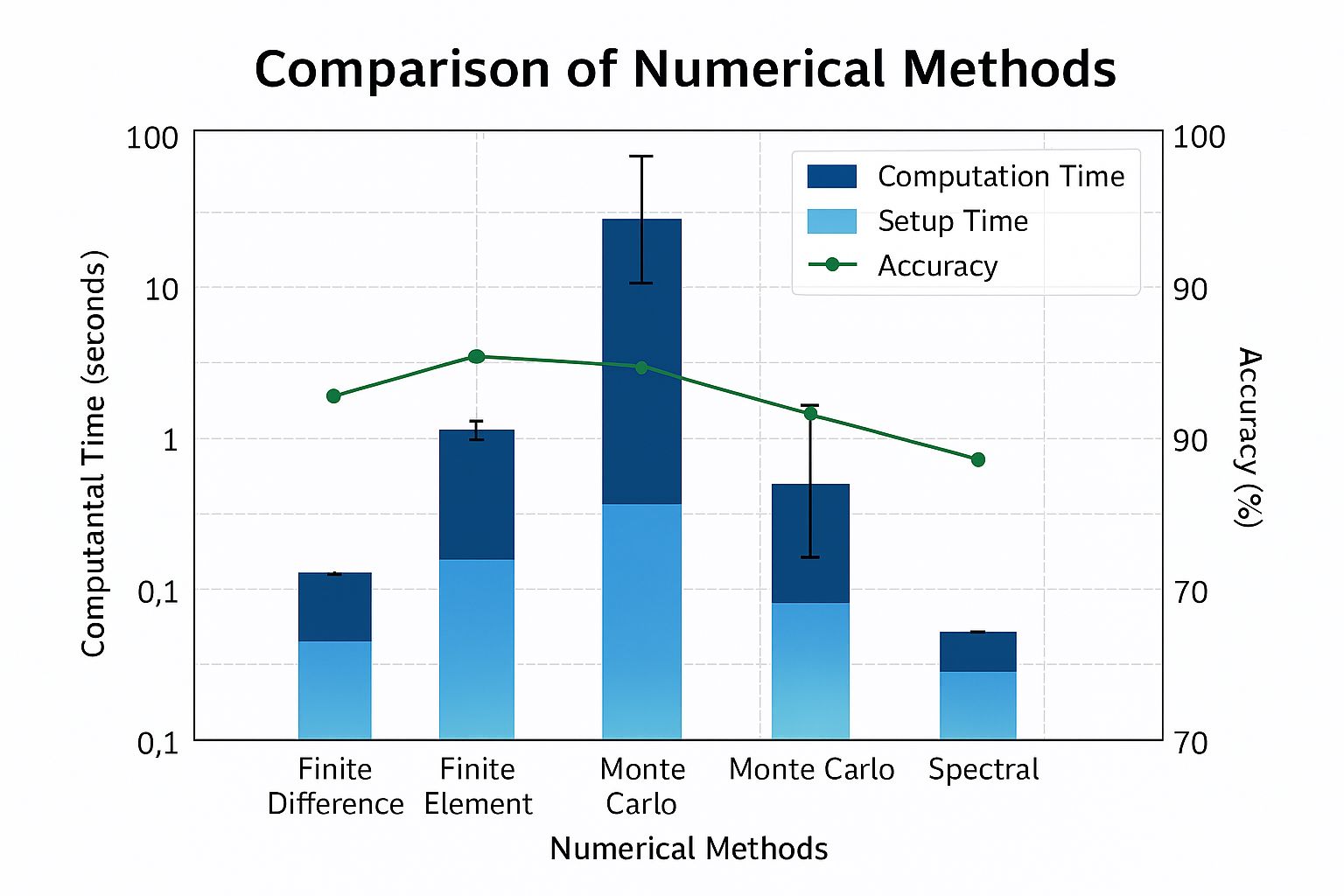
Computational performance comparison of different numerical methods
| Method | Time Complexity | Memory Usage | Parallel Scaling | Accuracy/Step |
|---|---|---|---|---|
| Explicit FD | O(N·M) | Low | Good | 1st-2nd order |
| Implicit FD | O(N³) | High | Poor | 2nd-4th order |
| Finite Element | O(N³) | High | Medium | High order |
| Monte Carlo | O(N) | Low | Excellent | O(1/√N) |
| Spectral | O(N log N) | Medium | Good | Exponential |
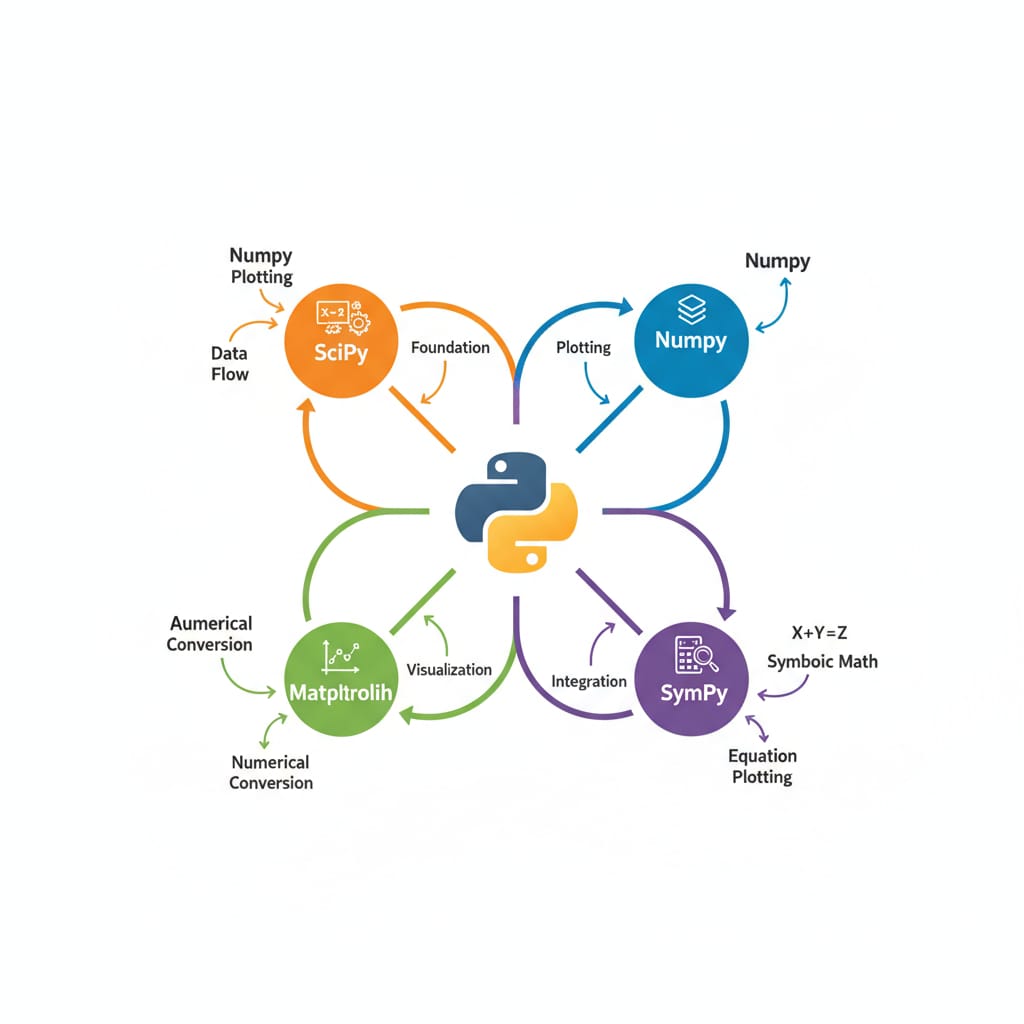
Python scientific computing library ecosystem
Numerical Computing
Foundation for numerical computing in Python. Provides N-dimensional arrays, linear algebra, and random number generation.
Scientific Computing
Advanced scientific computing modules: integration, optimization, interpolation, ODE solving, and signal processing.
Symbolic Mathematics
Symbolic computation library for algebra, calculus, discrete math, and physics. Useful for deriving equations analytically.
Matplotlib
2D/3D Plotting
Numba
JIT Compilation
FEniCS
FEM Solving
PyTorch
ML/Autodiff
pip install numpy scipy sympy matplotlib pip install jupyter notebook pip install numba fenics # Optional

Grid-based approximation with gradient calculations

Random sampling for high-dimensional integration

Wavefunctions and energy levels
Using neural networks as PDE solvers
GPU acceleration and parallel computing
Quantum computing for numerical methods
Interested in computational physics, AI research, or materials science? Check out my other research papers and projects.