The Universal Fragmentation Principle
Why does a glass cup, a rock, or even a bubble—when they break—produce fragments following a predictable mathematical pattern? This research from Aix‑Marseille University reveals a universal law that governs fragmentation across diverse materials and scenarios.

Visual representation of fragmentation: thousands of fragments following universal statistical patterns
Core Insight: Instead of focusing on material-specific fracture mechanics, the researchers propose that fragmentation follows a universal statistical law based on two fundamental principles:
- Conservation of Mass: The total mass/volume must be distributed among fragments
- Maximum Randomness: Under chaotic conditions, the most probable outcome maximizes disorder
From these principles, the researchers derived a mathematical formula that predicts fragment size distributions across different dimensionalities (3D solids, 2D plates, liquid shells, etc.).
Mathematical Foundation
The universal fragmentation law predicts a power-law distribution for fragment sizes:
N(s) ∝ s-α
where:
N(s) = number of fragments of size s
α = exponent depending on dimensionality (3D: α≈2.0, 2D: α≈1.5)
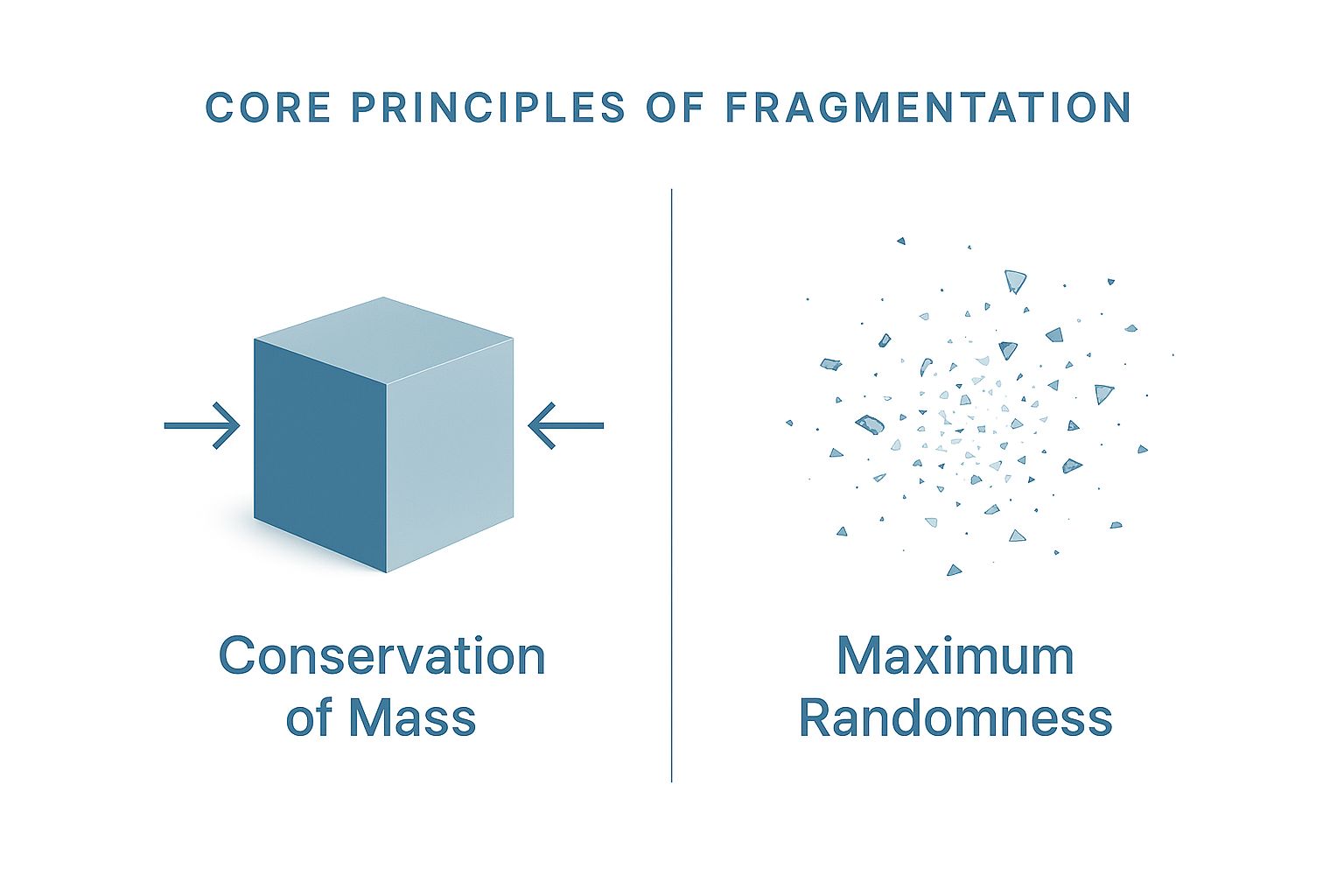
Infographic illustrating the core principles: mass conservation (left) and maximum randomness (right)
This power-law structure explains why there are many small fragments, fewer medium-sized ones, and very few large pieces—a pattern observed across countless fragmentation experiments.
Dimensional Consistency
The law elegantly adapts to different dimensionalities:
- 3D Solids: Blocks, spheres, cubes (e.g., sugar cubes, rocks)
- 2D Plates: Sheets, plates, thin layers
- 1D Shells: Liquid shells, bubbles, hollow structures
Experimental Validation
The researchers tested their theoretical predictions against extensive experimental data spanning decades of fragmentation research:
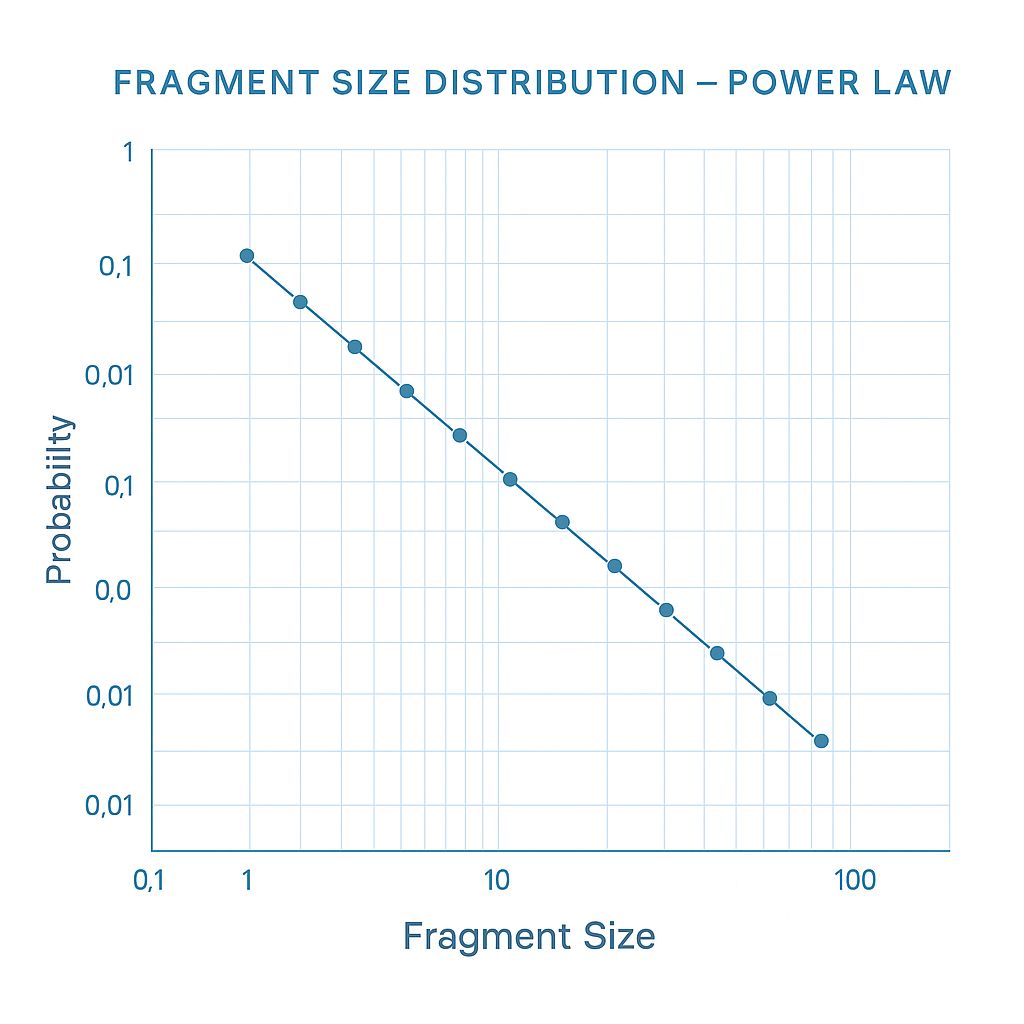
Log-log graph showing the characteristic power-law line of fragment size distribution

Experimental validation: Sugar cube fragmentation captured in high-speed photography
Retrospective Validation
- Brittle Solids: Glass, ceramics, rock fragmentation data
- Liquids & Bubbles: Droplet breakup, bubble bursting experiments
- Archaeological Evidence: Stone-tool flake distributions
- Plastic Debris: Environmental fragmentation patterns
New Controlled Experiment: Sugar Cubes
The team conducted a fresh experiment crushing sugar cubes—simple 3D solids with uniform structure. Their model's prediction matched the experimental fragment-size distribution with remarkable accuracy, providing strong validation for the theory.
Key Finding: The same mathematical law describes fragmentation in materials as different as glass, water, and stone—suggesting a universal underlying principle.
Limitations & Boundaries
While powerful, the universal fragmentation law has specific boundaries:
- Non-Random Breakup: Does not apply to regular, deterministic fragmentation (e.g., uniform droplet formation from capillary instability)
- Deformable Materials: Less accurate for highly ductile or soft materials where deformation dominates over fragmentation
- Shape Prediction: Describes size distribution but not fragment shape, which depends on material-specific crack propagation
- Ordered Structures: Materials with crystalline or highly ordered internal structure may show deviations
The law works best under "chaotic" or "random" fragmentation conditions—typical of most real-world breakage scenarios.
Implications & Applications
Scientific Unification
This work bridges multiple disciplines: materials science, fluid mechanics, geophysics, and statistical physics. It provides a common language for describing fragmentation phenomena across different fields.
Industrial Applications
- Mining & Comminution: Optimizing rock crushing processes for mineral extraction
- Materials Safety: Predicting debris sizes in failure scenarios for engineering design
- Recycling & Processing: Understanding and controlling material breakdown during recycling
- Geophysics: Modeling meteorite breakup, volcanic ash formation, and rock fragmentation
- Environmental Science: Understanding plastic degradation and microplastic formation
Philosophical Insight: This research demonstrates how apparent chaos in physical processes can conceal underlying order and predictability—a beautiful example of how fundamental principles can explain complex phenomena.
