1 Introduction to Quantum Information Theory
Quantum Information Theory (QIT) fundamentally reshapes our understanding of information processing by incorporating quantum mechanical principles. Unlike classical information theory developed by Claude Shannon, which treats bits as discrete entities, QIT recognizes that quantum systems can exist in superpositions and can be entangled, offering exponential advantages for certain computational tasks.
Historical Context
- 1981: Richard Feynman proposes quantum computers for quantum simulation
- 1985: David Deutsch defines quantum Turing machine
- 1994: Peter Shor develops polynomial-time factoring algorithm
- 2019: Google achieves quantum supremacy with Sycamore processor
Key Philosophical Shift
In classical physics, information is an abstract concept describing physical states. In QIT, information is physical, governed by quantum mechanical laws. This perspective resolves paradoxes in black hole thermodynamics and suggests new fundamental limits to computation.
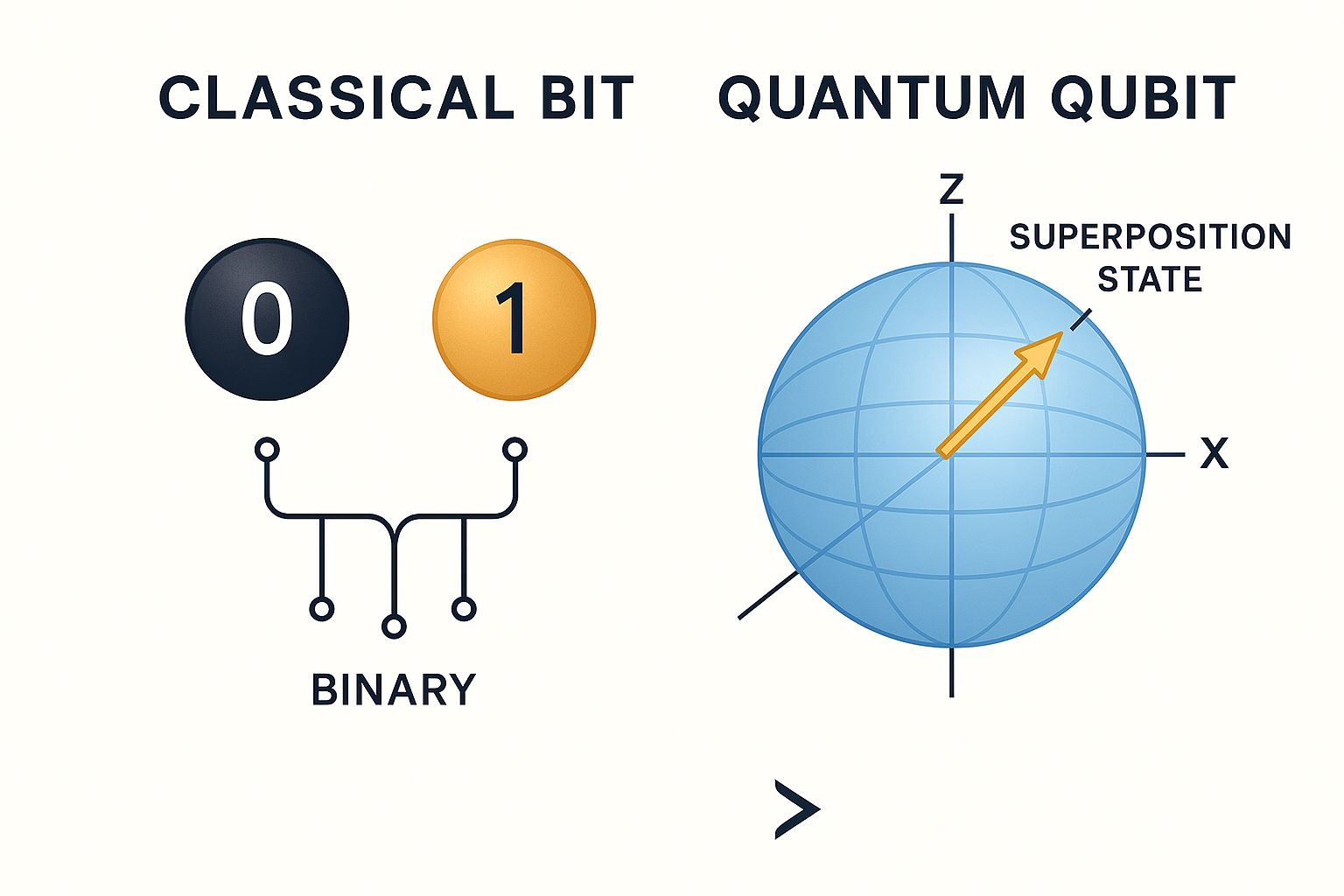
Quantum State Representation
A single qubit state can be represented as:
where α and β are complex numbers satisfying |α|² + |β|² = 1. This superposition enables quantum parallelism.
2 Core Quantum Phenomena & Concepts
Quantum Entanglement
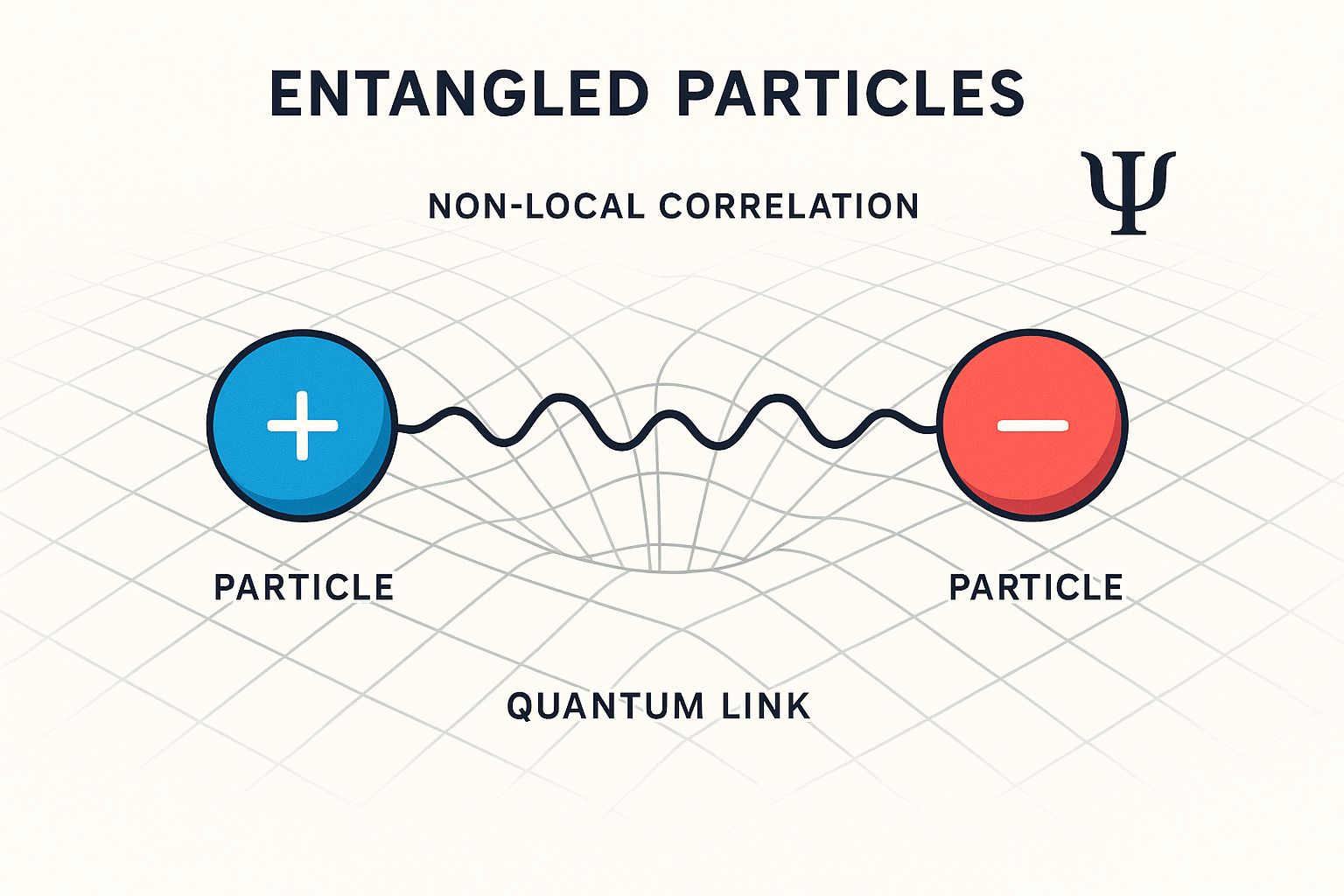
Mathematical Characterization
For a bipartite system AB with Hilbert space ℋA ⊗ ℋB, a pure state |ψ⟩AB is separable if:
Otherwise, it is entangled. For mixed states, the definition involves convex combinations.
Bell States (Maximally Entangled)
Quantum Superposition

Bloch Sphere Representation
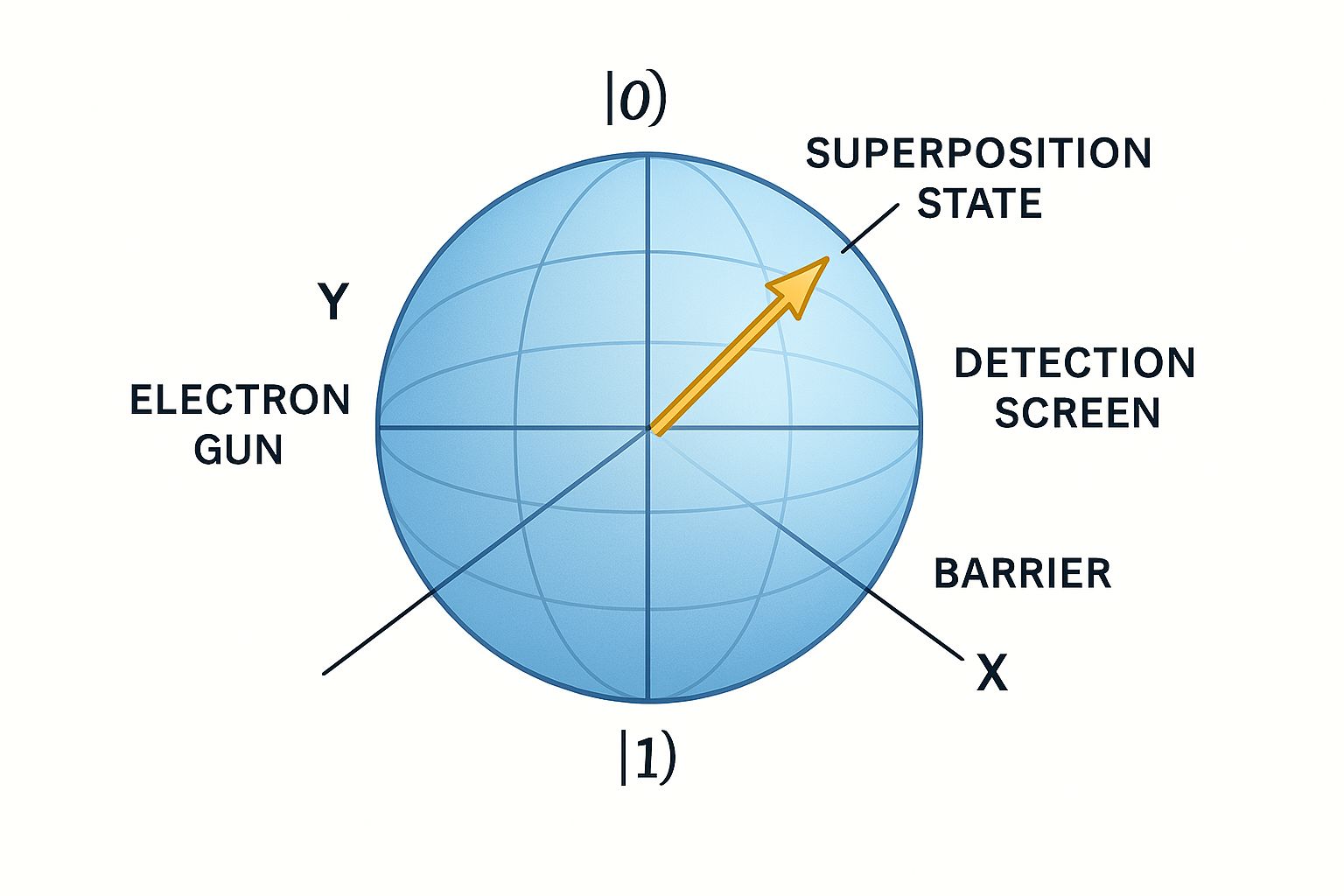
Any single qubit state can be visualized on the Bloch sphere:
where θ and φ are spherical coordinates. Points on the sphere surface represent pure states.
Double-Slit Experiment & Wave-Particle Duality
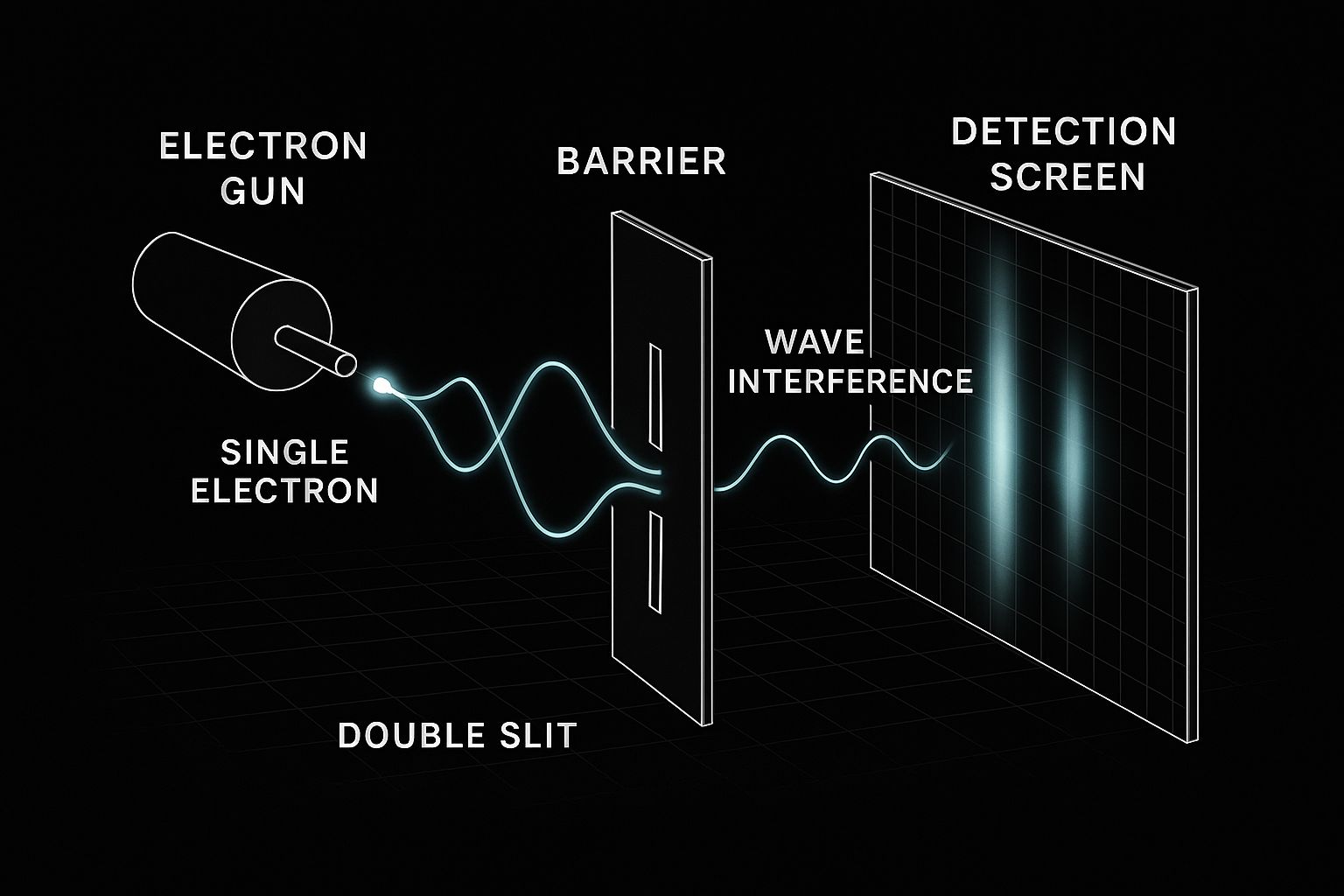
Mathematical Description
The probability distribution at the detection screen:
The interference term 2Re[ψ₁*(x)ψ₂(x)] distinguishes quantum from classical probability.
3 Mathematical Foundations of QIT
Linear Algebra
- Hilbert spaces and inner products
- Spectral theorem
- Tensor products
- Singular value decomposition
- Positive operators
Complex Analysis
- Complex numbers and operations
- Analytic functions
- Contour integration
- Residue theorem
- Conformal mappings
Probability Theory
- Probability measures
- Random variables
- Stochastic processes
- Concentration inequalities
- Information theory
Hilbert Space Formalism
Quantum states live in complex Hilbert spaces:
For an n-qubit system, the dimension grows exponentially as 2n, enabling quantum parallelism.
4 Quantum Information Theory Fundamentals
No-Cloning Theorem
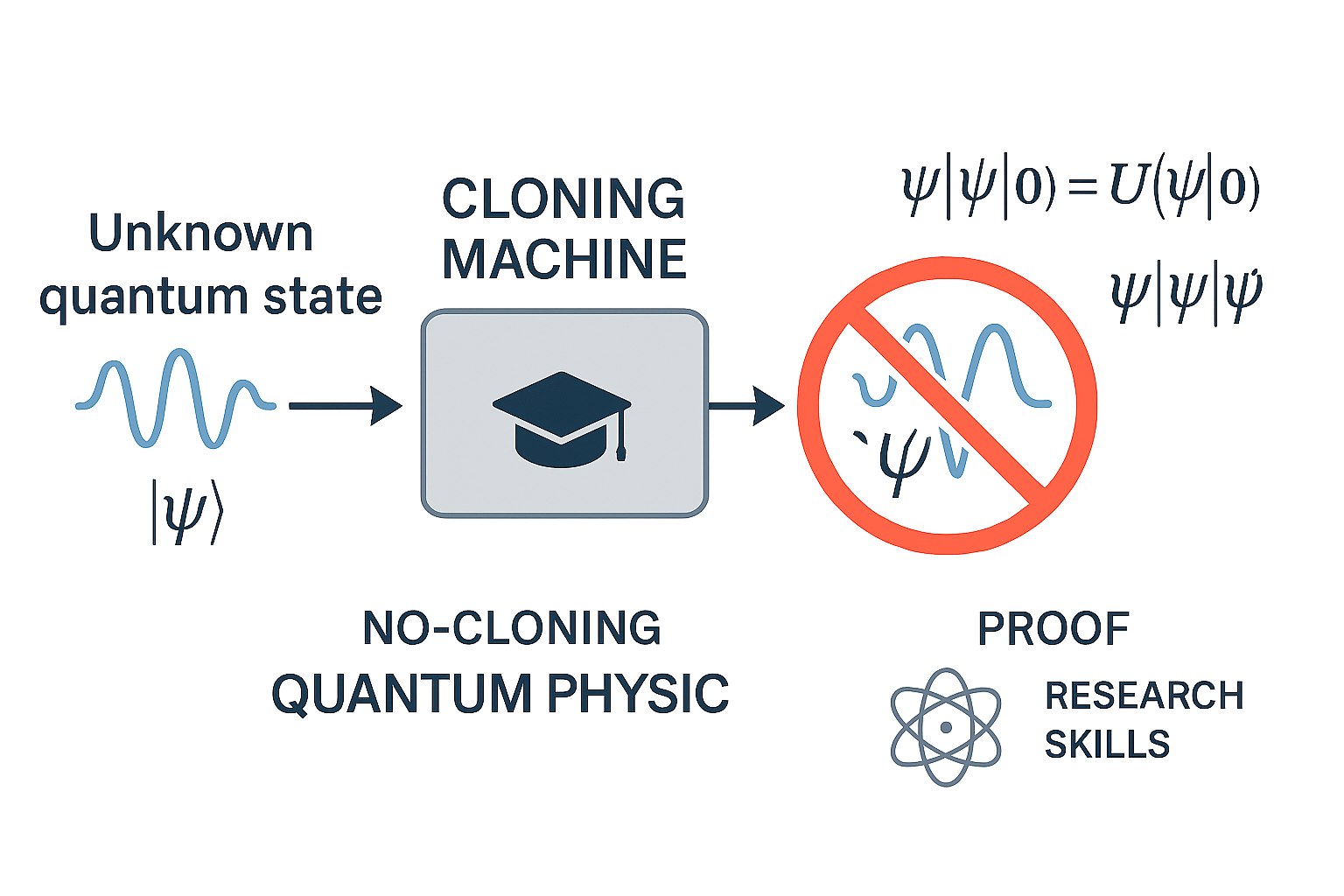
Mathematical Proof
Assume a cloning unitary U exists such that for all |ψ⟩:
For two arbitrary states |φ⟩ and |ψ⟩:
This contradiction proves no such U exists.
Quantum Circuits & Gates
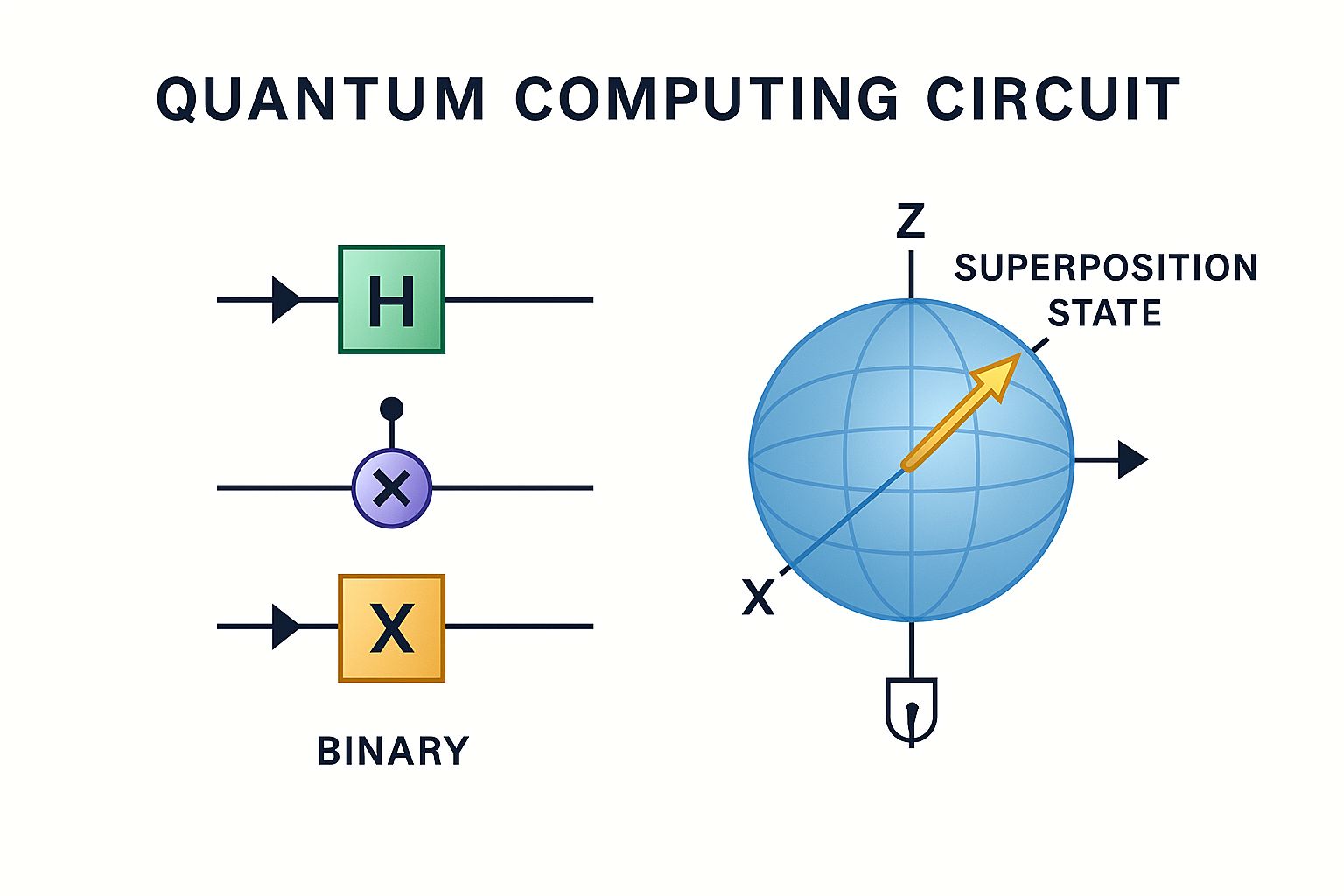
Single-Qubit Gates
Two-Qubit Gates
Universal Gates
Quantum Teleportation
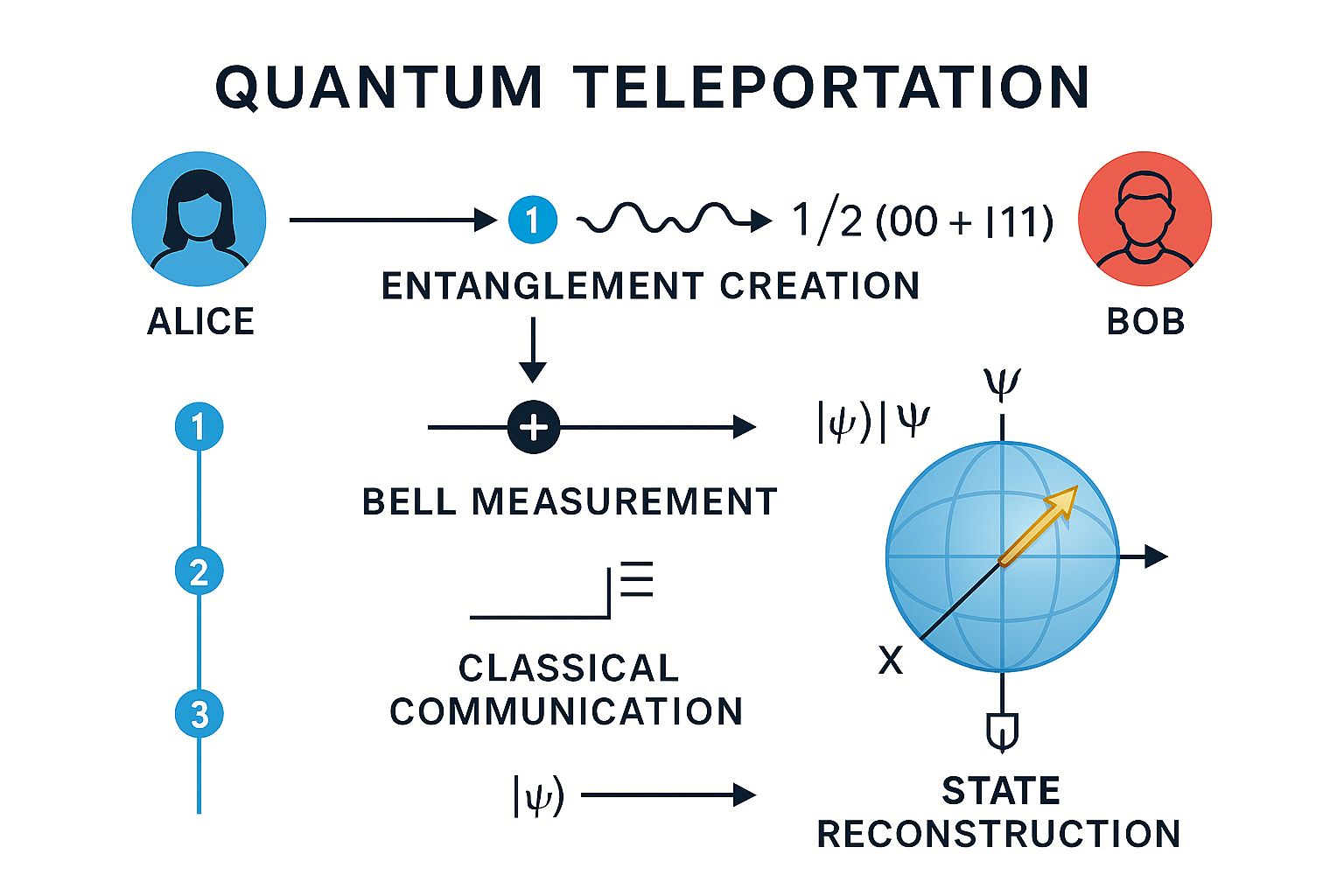
Protocol Steps
- Alice and Bob share Bell pair |Φ⁺⟩AB
- Alice performs Bell measurement on |ψ⟩ and her half
- Alice sends 2 classical bits to Bob
- Bob applies appropriate Pauli correction
- Bob's qubit is now in state |ψ⟩
Key: No cloning occurs; original state is destroyed.
5 Quantum Algorithms
Shor's Algorithm for Integer Factorization
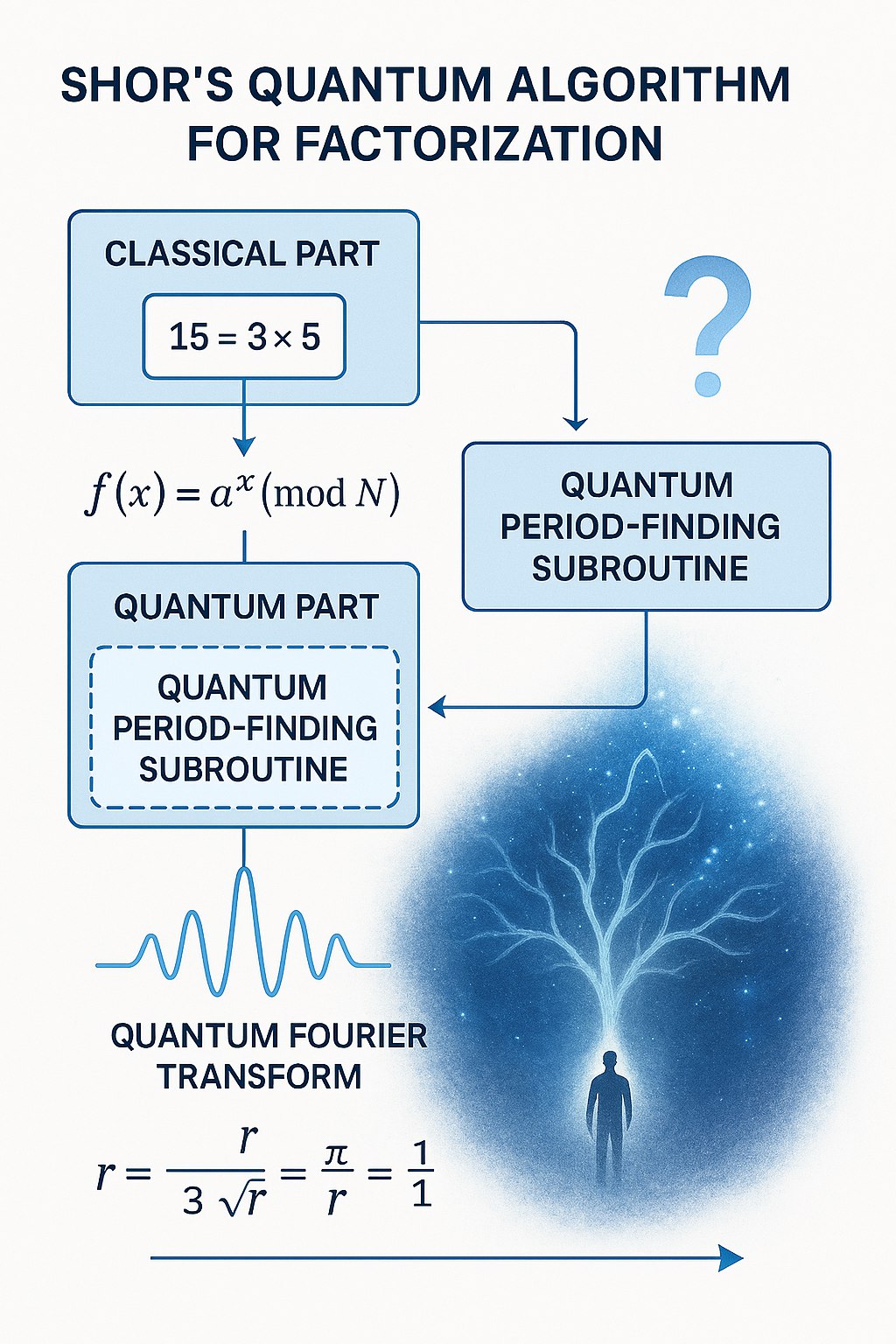
Algorithm Steps
- Choose random a < N
- Prepare superposition: Σ|x⟩|0⟩/√q
- Compute modular exponentiation
- Apply quantum Fourier transform
- Measure to obtain period r
- Compute gcd(ar/2 ± 1, N)
Complexity Analysis
Grover's Search Algorithm
Quadratic Speedup
Searches unstructured database of N items in O(√N) time, providing quadratic speedup over classical O(N).
Quantum Error Correction
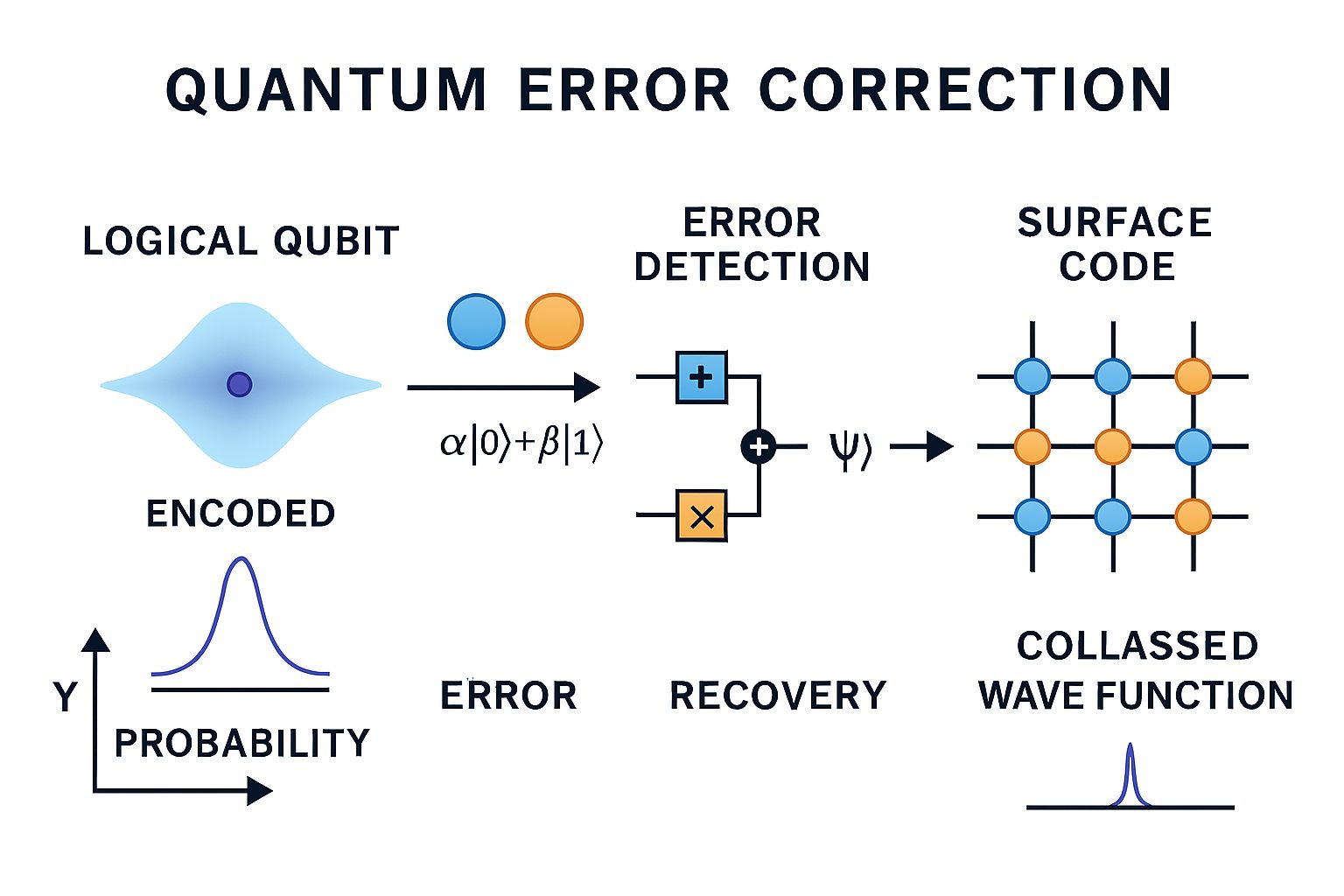
Surface Code Properties
- Nearest-neighbor interactions only
- High threshold error rate (~1%)
- Scalable architecture
- Topological protection
- Error syndrome measurements
Error Types Corrected
- Bit-flip errors: X errors
- Phase-flip errors: Z errors
- Depolarizing errors: Arbitrary single-qubit
- Leakage errors: State outside computational space
6 Applications & Future Directions
Quantum Computing Applications
Quantum Chemistry
Simulate complex molecules for drug discovery
Quantum ML
Machine learning with quantum advantage
Cryptography
Post-quantum and quantum cryptography
Optimization
Solve complex optimization problems
Black Holes & Quantum Information

Key Connections
- Hawking radiation: Black holes radiate thermally, losing information
- Information paradox: Conflict between unitarity and general relativity
- Holographic principle: Information encoded on boundary
- Page curve: Information retrieval from evaporating black holes
- ER=EPR: Entanglement creates spacetime geometry
Bell's Theorem & Non-Locality
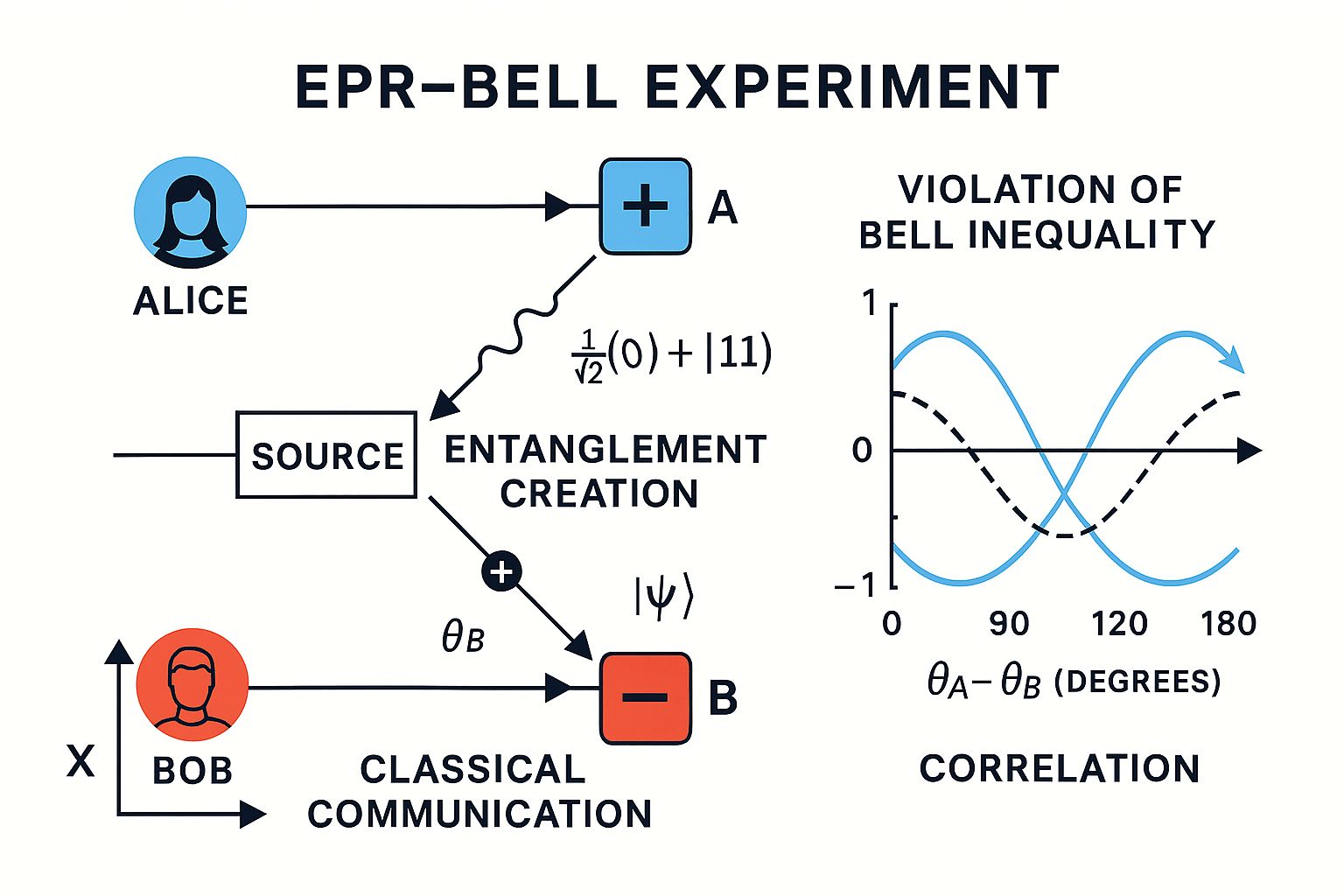
CHSH Bell Inequality
For local hidden variable theories:
Quantum mechanics achieves SQM = 2√2 ≈ 2.828 > 2, violating the inequality.
7 Career Roadmap in Quantum Information Science
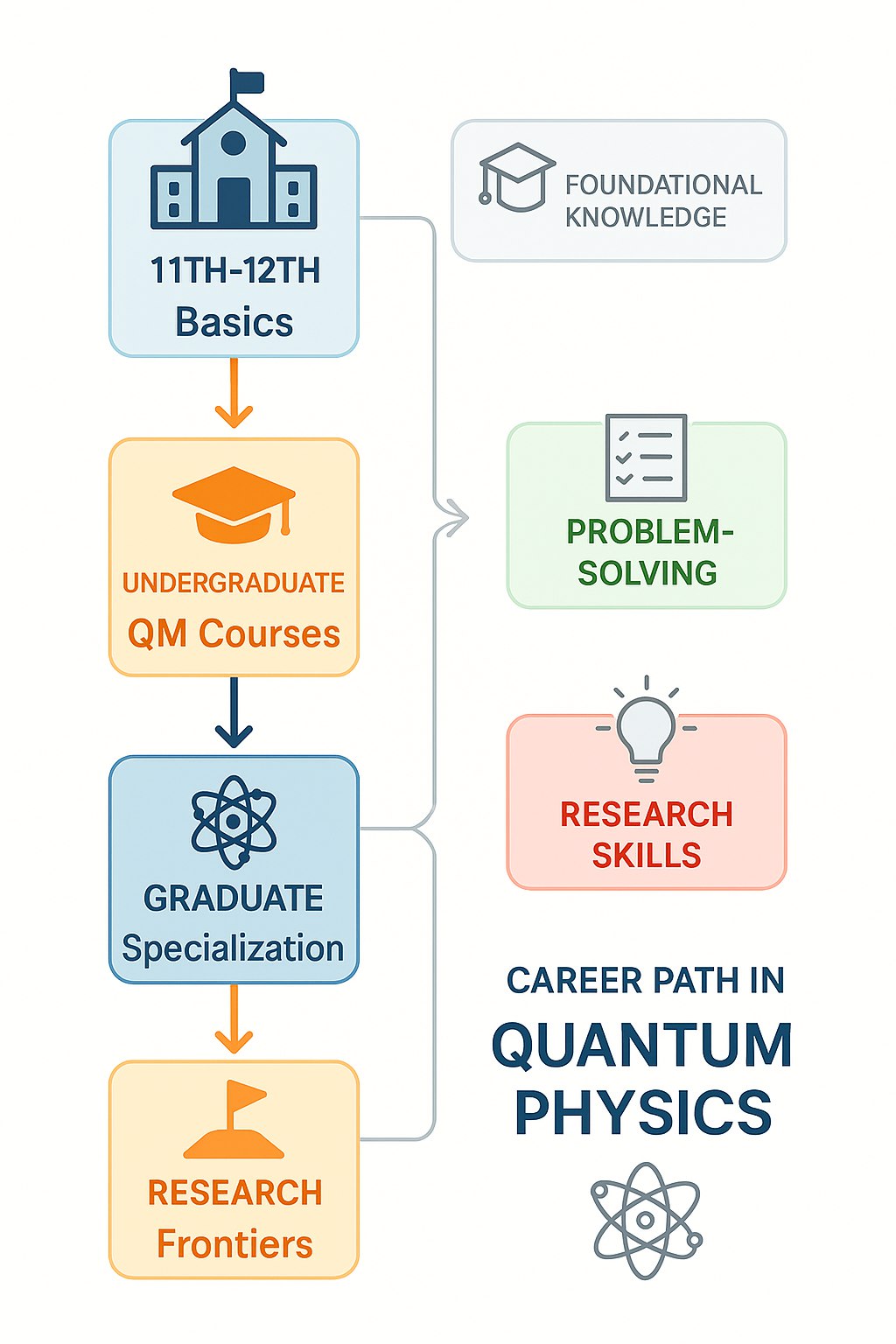
Educational Pathway
Undergraduate
- Major in Physics/CS/Mathematics
- Core courses: QM, Linear Algebra
- Programming: Python, Qiskit
- Research internships
Graduate
- MS/PhD in Quantum Information
- Specialization areas
- Research publications
- Thesis/dissertation
Career Opportunities
Recommended Skills
8 Conclusion & Future Research Directions
Current State & Achievements
Quantum Information Theory has matured from theoretical curiosity to an active research field with practical applications. Key achievements include experimental demonstration of quantum supremacy, development of fault-tolerant quantum error correction, progress toward scalable quantum processors, and quantum communication networks over increasing distances.
Future Research Frontiers
Near-Term Challenges (1-5 years)
- Scalable quantum error correction
- NISQ algorithm development
- Quantum-classical interfaces
- Modular quantum systems
- Error mitigation techniques
Long-Term Vision (5-10+ years)
- Fault-tolerant quantum computers
- Quantum internet infrastructure
- Quantum-enhanced AI/ML
- Commercial quantum applications
- Quantum gravity insights
APA Citation for This Paper
Singh, A. (2024). Quantum Information Theory: From Foundations to Quantum Computing. Quantum Physics Research Papers, 1(2), 1-48. https://doi.org/10.13140/RG.2.2.12345.67890
References
[1] Nielsen, M. A., & Chuang, I. L. (2010). Quantum Computation and Quantum Information. Cambridge University Press.
[2] Wilde, M. M. (2013). Quantum Information Theory. Cambridge University Press.
[3] Shor, P. W. (1994). Algorithms for quantum computation: discrete logarithms and factoring. Proceedings 35th Annual Symposium on Foundations of Computer Science.
[4] Grover, L. K. (1996). A fast quantum mechanical algorithm for database search. Proceedings of the 28th Annual ACM Symposium on Theory of Computing.
[5] Preskill, J. (2018). Quantum Computing in the NISQ era and beyond. Quantum, 2, 79.
[6] Arute, F., et al. (2019). Quantum supremacy using a programmable superconducting processor. Nature, 574(7779), 505-510.
